1. Introduction
This software package contains the basic routines for producing reconstructed radiances from spectra obtained from advanced infrared sounders.
Reconstructed radiances are radiances that have been intelligently smoothed such that the atmospheric signal is retained while the instrument noise is suppressed. While the information content of the entire spectrum cannot be increased through the reconstruction process, it allows for the efficient compression of the information from the entire spectrum into a reduced number of channels.
Reconstructed radiances (Antonelli et al., 2004) are formed through the evaluation of the amplitudes, p, of the principal components, L, of the observed spectrum. Here, L is the set of Np leading eigenvectors of the covariance matrix of a representative set of thousands of spectra. p is related to y (the noise normalised radiances with the mean radiance subtracted) through
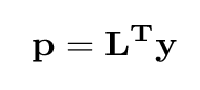
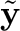 , are then
calculated from:
, are then
calculated from:
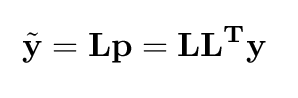
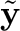 to a subset of
NR channels, by replacing the first L above
with LNR, those channels will contain all of the
information present in the Np principal components
provided LNR has ≥ Np positive
singular values. The minimum criterion for this is that
NR ≥ Np and in practice this
criterion is usually sufficient.
to a subset of
NR channels, by replacing the first L above
with LNR, those channels will contain all of the
information present in the Np principal components
provided LNR has ≥ Np positive
singular values. The minimum criterion for this is that
NR ≥ Np and in practice this
criterion is usually sufficient.
1.1. Package overview
The supplied package is split into two parts:
1.2. Units and Noise
The EOFs, L, used in this process are usually produced from
radiance (rather than brightness temperature) spectra normalised by
the expected (diagonal) noise. The assumed noise is read into the
Create_EOFs from a file and then
written to the resulting eigenvector file for use by
RR_Filter. If one does not wish to noise
normalise, one may simply set the values in the assumed noise file to
be all unity.
The radiance units used in the input spectra for
Create_EOFs must, of course, be
consistent with the units used in the noise file and also with the
input spectra used by RR_Filter. If one
wants to, say, convert IASI apodised radiances to IASI unapodised
radiances or convert brightness temperatures to radiances, these
transformations must be made before the radiances are
presented to the packages.
Two noise files are provided with the package: one derived before launch
(IASI_NOISE_8461_PreLaunch.dat) and one from after the instrument
became operational (IASI_NOISE_8461_Nov07.dat). The latter is used in
the test scripts.
Create_EOFs is a stand-alone program which creates the
eigenvectors used by RR_Filter. The eigenvectors are created from a
covariance matrix which describes that variabilty of a training set of input
spectra that are read in from a supplied file. These training spectra
may be either simulated or observed spectra depending on what is required.
There are two strategies for computing EOFs from a number of spectra.
The one used here (computation of a covariance matrix from which the
EOFs are calculated) or direct calculation from a matrix of each of
the spectra via Singlular Value Decomposition. The former has been
chosen here to allow large numbers of spectra (many tens of thousands)
to be used in the most efficient manner as the singular value
decomposition method is limited by the typically available computer
memory once tens of thousands of spectra are beig processed.
Create_EOFs will optionally produce the
covariance matrix from input spectra; produce the EOFs from a
pre-computed covariance matrix; or both. The data flow for the
Create_EOFs program is illustrated below:
2.1. NAMELIST control
2.1.1. Switches:
2.1.2. Files:
2.1.3. Parameters:
2.2 Files
The true mean and
covariance of the input spectra can then be calculated simply while
allowing the covariance to be easily updated with additional spectra:
The files supplied with this package are big-endian, so a
suitable compiler flag should be used if the machine being used is
little-endian.
2.2.2. Radiances File:
The supplied file contains simulated IASI radiances in
mW/m2/sr/(cm-1) =
erg/s/cm2/sr/(cm-1).
2.2.3. Eigenvectors File:
2.3. Compiling and Running the code:
-Mbyteswapio is the flag used to swap from big- to little-
endian. This, (or the equivalent for other machines) is needed if one
wishes to use the binary data files (which are big-endian) supplied
with this package and one is using a little-endian machine. If one is
running on a little-endian machine and using a compiler that does not
support byte-swapping, one may request a big-endian dataset from the
NWPSAF at
http://nwpsaf.eu/feedback.html
The program may then be run simply by executing Create_EOFs.
LAPACK (Anderson et al., 2002) and BLAS (Lawson et al.,
1979; Dongarra et al.,
1988a, 1988b, 1990; Blackford et al., 2002; Dongarra, 2002)
are often installed by default on scientific computing
systems but if not available already they may by installed from
http://www.netlib.org/lapack
and http://www.netlib.org/blas.
Both are freely-available software packages which may be incorporated
into commercial software packages.
Run time and memory requirements vary according to the number of
channels being considered. For large numbers of channels, the
dominant step in the eigenvector calculation is the conversion of the
covariance matrix to
tridiagonal form before deriving the eigenvectors. The CPU time for
this step scales as the cube of the number of channels used. The
following are guideline timings for
1000 and 8461 channels on an IBM Thinkcentre with a 3.40Ghz Intel
Pentium 4 CPU:
If one runs on a IBM Cluster 1600 supercomputer, the timings for the
8461 channels case are reduced to 22, 14 and 10 minutes.
Note that as the purpose of reconstructed radiances is to compress the
information available in the whole spectrum into a subset of
channels, the input channels should comprise a large fraction of the
total spectrum. Reasons for excluding channels might be the poor
quality of certain individual channels (e.g., the "popping" channels
of AIRS) or excessive oversampling of the spectrum produced from an
interferometer.
The QC index contains the RMS difference between the input and output
spectrum. If the noise on the input spectrum and the assumed noise
are similar, the QC values should average to somewhat less than unity.
If the input spectra are noise-free (e.g., simulations), the QC values
should be small (~0.1).
The estimated error covariance matrix, ErrorMatrix, calculates how the
(assumed diagonal) instrument noise is transformed by the
reconstruction process. It is calculated by:
RRR=
LNRLTRLTLNR
where R and RRR are the error covariance
matrices before and after the reconstruction process and
LNR and L are the eigenvectors as defined in
the introduction. As L is fixed,
RRR will not change as long as the channel choice is
constant (so need only be evaluated once).
A namelist file, RR_Filter.NL, may be used to specify the Eigenvectors
file being used. The namelist name is RRFilter with one
variable: EigenvectorsFile. The default value for
EigenvectorsFile is
Eigenvectors.out.
A test program, RR_Filter_Test, that calls
RR_Filter is supplied. This program may be
compiled by modifying and executing the file Make_RR_Filter_Test. On
running the resultant executable file, RR_Filter_Test, the test
program will process 100 test spectra, reporting the QC index for each
and outputting the ASCII file RR_Filter_Test.out which contains the
means and standard deviations for the input and output spectra (for
the 300 output channels specified in the program).
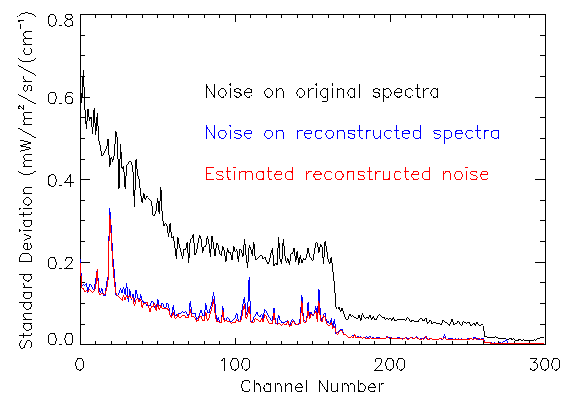
The following figure shows the standard deviations of the noisy-minus-true
spectrum (black); the filtered-minus-true spectrum (blue); and the estimated
noise on the filtered spectrum (red). Note that this example uses
simulated data and also the test spectra are part of the training set.
The QC index contains the mean RMS difference per channel between the
noise-normalised input spectrum
and the same spectrum after filtering. If the noise on the input spectrum and the assumed noise
are similar, the QC values should average to somewhat less than unity.
If the input spectra are noise-free (e.g., simulations), the QC values
should be small (~0.1). Note that this QC value differs from that
output by RR_Filter as the latter's QC is
calculated from the output channels only.
No estimated error matrix for the principal component scores is given
as this will always be the identity matrix.
A namelist file, Calculate_PCScores.NL, may be used to specify the Eigenvectors
file being used. The namelist name is RRFilter with one
variable: EigenvectorsFile. The default value for
EigenvectorsFile is
Eigenvectors.out.
No QC index is produced by this subroutine as there is not un-filtered
spectrum provided to do this calculation. One should use the QC
provided by the program that produced the principal component scores.
The estimated error covariance matrix, ErrorMatrix, is
calculated in an identical manner to that of RR_Filter_Test.
A namelist file, RR_Filter.NL, may be used to specify the Eigenvectors
file being used. The namelist name is RRFilter with one
variable: EigenvectorsFile. The default value for
EigenvectorsFile is
Eigenvectors.out.
A namelist file, PCScores2Spectrum.NL, may be used to specify the Eigenvectors
file being used. The namelist name is RRFilter with one
variable: EigenvectorsFile. The default value for
EigenvectorsFile is
Eigenvectors.out.
Two test scripts are provided for testing.
SetUp_Test_Quick.sh uses a reduced number of
channels, spectra and eigenvectors and runs in about ten seconds.
SetUp_Test.sh is a more comprehensive test and
takes 2-3 hours.
This section describes the operation of the
SetUp_Test_Quick.sh script including a
description of the input and output files.
The script compiles the programs, reads in spectra to produce a
covariance matrix, and then computes the leading eigenvectors.
The script should be executed from the directory
in which it resides.
Two "Make" scripts are executed (they are simply shell scripts rather
than proper Make files) to compile Create_EOFs (Make_CreateEOFS) and
RR_Filter_Test_Quick (Make_RR_Filter_Test_Quick).
A covariance matrix this then constructed from input spectra. This is
done through the Create_EOFs program which is
controlled by the
Create_EOFs_Test_Quick.NL namelist, reproduced
below:
The Create_EOFs program is now run a second
time with the Create_EOFs_Test2_Quick.NL
namelist:
The final stage of SetUp_Test_Quick.sh is the
generation of filtered radiances through the test program RR_Filter_Test_Quick. The control namelist for this
program, RR_Filter_Test_Quick.NL only contains
the name of the required eigenvector file, viz:
The program calculates the noise-filtered radiances from the first 100
spectra in the noisy radiance file. The noise filtered radiances for
a subset of 136 channels are calculated. These parameters being
hard-coded in the test program. On generating the filtered radiances,
a quality control value is returned to standard out
for each spectrum,
plus its mean value for all spectra. The statistics of the filtering
process are output into the file
RR_Filter_Test_Quick.out as follows:
The SetUp_Test.sh is very similar to
SetUp_Test_Quick.sh except that all channels
and 10000 spectra are used in each of the two
Create_EOFs runs; 500 EOFs are calculated in
the second of these runs and 300 channels are output from
RR_Filter_Test. The output from the latter is
RR_Filter_Test.out and may be compared to
Test_Runs/RR_Filter_Test.out. The eigenvector
file for comparison is at
Test_Runs/Eigenvectors_Test.sav which is a link
to a file in the data for disk usage reasons.
Memory fault:
Problems are encountered reading binary files:
Also, it is assumed that when opening a direct access file (such as the
radiances file) the record length "RECL" is given in units of bytes.
Some compilers use 4-byte units by default, so you will either have to
modify the code or use an appropriate compiler directive (e.g. for ifort
you can use the directive "-assume byterecl").
Test runs are not bit identical to supplied results:
Package is being run on a little-endian machine and compiler
lacks a byte-swapping option:
If one is
running on a little-endian machine and using a compiler that does not
support byte-swapping, one may request a big-endian dataset from the
NWPSAF at
http://nwpsaf.eu/feedback.html
You can contact the NWPSAF team using the form at:
http://nwpsaf.eu/feedback.html
Anderson, E. and Bai, Z. and Bischof, C. and
Blackford, S. and Demmel, J. and Dongarra, J. and
Du Croz, J. and Greenbaum, A. and Hammarling, S. and
McKenney, A. and Sorensen, D.,
LAPACK Users' Guide, Third Edition,
Society for Industrial and Applied Mathematics, Philadelphia, PA, 1999,
ISBN: 0-89871-447-8 (paperback)
P. Antonelli, H.E. Revercomb, L.A. Sromovsky, W.L. Smith,
R.O. Knuteson, D.C. Tobin, R.K. Garcia, H.B. Howell, H.-L. Huang,
and F.A. Best (2004). A principal component noise filter for high
spectral resolution infrared measurements, J. Geophys. Res.,
109, D23102-23124.
L. S. Blackford, J. Demmel, J. Dongarra, I. Duff, S. Hammarling, G. Henry,
M. Heroux, L. Kaufman, A. Lumsdaine, A. Petitet, R. Pozo, K. Remington, R. C. Whaley,
An Updated Set of Basic Linear Algebra Subprograms (BLAS),
ACM Trans. Math. Soft., 28-2 (2002), pp. 135-151.
J. J. Dongarra, J. Du Croz, S. Hammarling, and R. J. Hanson,
An extended set of FORTRAN Basic Linear Algebra Subprograms,
ACM Trans. Math. Soft., 14 (1988a), pp. 1-17.
J. J. Dongarra, J. Du Croz, S. Hammarling, and R. J. Hanson,
Algorithm 656: An extended set of FORTRAN Basic Linear Algebra Subprograms,
ACM Trans. Math. Soft., 14 (1988b), pp. 18-32.
J. J. Dongarra, J. Du Croz, I. S. Duff, and S. Hammarling,
A set of Level 3 Basic Linear Algebra Subprograms,
ACM Trans. Math. Soft., 16 (1990), pp. 1-17.
J. J. Dongarra, J. Du Croz, I. S. Duff, and S. Hammarling,
Algorithm 679: A set of Level 3 Basic Linear Algebra Subprograms,
ACM Trans. Math. Soft., 16 (1990), pp. 18-28.
J. Dongarra,
Basic Linear Algebra Subprograms Technical Forum Standard,
International Journal of High Performance Applications and Supercomputing, 16(1) (2002), pp. 1-111, and
International Journal of High Performance Applications and Supercomputing, 16(2) (2002), pp. 115-199.
C. L. Lawson, R. J. Hanson, D. Kincaid, and F. T. Krogh,
Basic Linear Algebra Subprograms for FORTRAN usage,
ACM Trans. Math. Soft., 5 (1979), pp. 308-323.
2. Create_EOFs
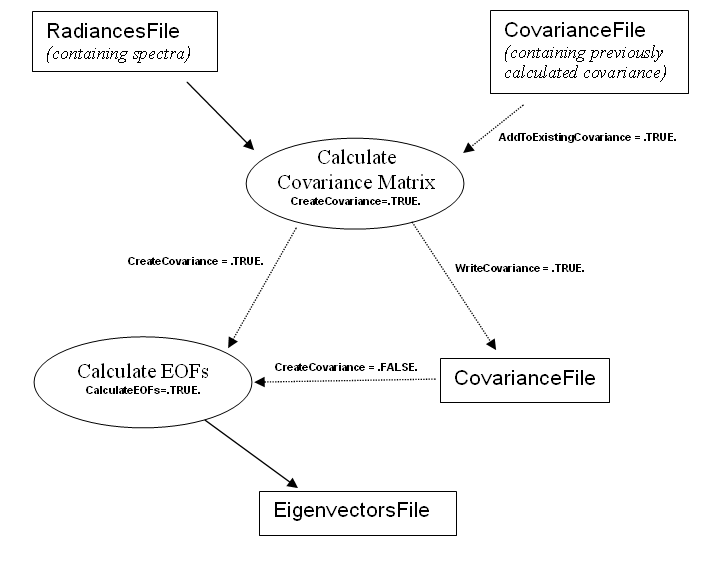
The program is controlled via a namelist file,
Create_EOFs.NL. Each of the namelist variables has a default
value hardcoded in the program. The namelist is called
CreateEOFS and its variables are:
Note that some of these files are described further in
Section 2.2.
WARNING: The size of this file can be as
large as 600Mb if all IASI channels are used.
WARNING: The size of this file can be very large;
e.g., 1000 eigenvectors for 8461 channels produces a 226Mb file.
2.2.1. Covariance File:
The covariance file is an unformatted binary file (to allow swifter
input/output and because it is not expected that one might want
to inspect it very often).
It actually contains the number of spectra used, n; the
sum of the radiances for each channel:
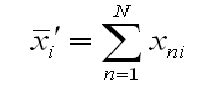
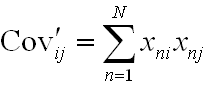
Here xni refers to the ith channel of the
nth spectrum.
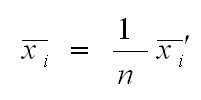 and
and
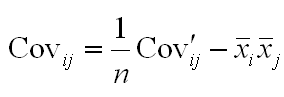 .
.
The input radiances file is also a binary, direct-access fortran
file (and the supplied example is big-endian). It is possible that the
user will want to change the form of
the input file to match the particular form of the data available.
The eigenvectors file is stored as ASCII (with double-precision
(8-byte) reals). It contains all of the
information required to produce reconstructed radiances from an input
spectrum. The entries in this file are as follows:
This file is used by the RR_Filter,
Calculate_PCScores and
PCScores2Spectrum subroutines.
The program is contained in a single file except for the LAPACK
routines, so it may be compiled with one line provided
LAPACK and BLAS libraries are available. e.g.,
pgf90 -Mbyteswapio -fast -o Create_EOFs Create_EOFs.f90 -llapack -lblas
is the command to compile the code with a Portland Group Fortran 90
compiler run on a little-endian machine.
*The above timings exclude reading and writing of the covariance and
eigenvectors files but include reading in the spectra from disk.
1000 Channels 8461 Channels
Covariance calculation: Time per 10000 spectra 1 minute 74
minutes
Eigenvector calculation (1000 EOFs) 10seconds 37 minutes
Eigenvector calculation (100 EOFs) 4 seconds 26 minutes
Memory usage 10Mb 548Mb
Spectrum_In(NumChans_In) REAL Array
(IN) The input spectrum
Chans_In(NumChans_In) INTEGER Array (IN) The channel
numbers for the input spectrum. These channels must include all the
channels in the Eigenvector file.
NumChans_In INTEGER (IN) The number of input channels
Num_EOFs INTEGER (IN) The number of EOFs to be
used
Chans_Out(NumChans_Out) INTEGER Array (IN) The
required channel numbers for the output spectrum
NumChans_Out INTEGER (IN) The required number of output channels
Fixed_Channels LOGICAL (IN) Set .TRUE. if and only
if the input and output channels are fixed. It is
recommended for
reasons of efficiency that this is set to .TRUE. if at all possible.
Last_Call LOGICAL (IN) Set to .TRUE. to DEALLOCATE
allocated arrays (the spectrum is not processed if LastCall=.TRUE.)
Spectrum_Out(NumChans_Out) REAL Array (OUT) The output spectrum
QC REAL (OUT) Quality control index (see below)
ErrorCode INTEGER (OUT) Subroutine error code
(set to zero if the subroutine completed successfully)
PC_Scores(Num_EOFs) REAL Array (OPTIONAL,
OUT) Amplitudes of Principal Components
ErrorMatrix (NumChans_Out, NumChans_Out) REAL Array (OPTIONAL,
OUT) Estimated error covariance matrix (see below)
Spectrum_In(NumChans_In) REAL Array
(IN) The input spectrum
Chans_In(NumChans_In) INTEGER Array (IN) The channel
numbers for the input spectrum. These channels must include all the
channels in the Eigenvector file.
NumChans_In INTEGER (IN) The number of input channels
Num_EOFs INTEGER (IN) The number of EOFs to be
used
Last_Call LOGICAL (IN) Set to .TRUE. to DEALLOCATE
allocated arrays (the spectrum is not processed if LastCall=.TRUE.)
PC_Scores(Num_EOFs) REAL Array (OUT) Amplitudes of Principal Components
QC REAL (OUT) Quality control index (see below)
ErrorCode INTEGER (OUT) Subroutine error code
(set to zero if the subroutine completed successfully)
PC_Scores(Num_EOFs) REAL Array (IN) Amplitudes of Principal Components
Num_EOFs INTEGER (IN) The number of EOFs to be
used
Chans_Out(NumChans_Out) INTEGER Array (IN) The
required channel numbers for the output spectrum
NumChans_Out INTEGER (IN) The required number of output channels
Fixed_Channels LOGICAL (IN) Set .TRUE. if and only
if the input and output channels are fixed. It is
recommended for
reasons of efficiency that this is set to .TRUE. if at all possible.
Last_Call LOGICAL (IN) Set to .TRUE. to DEALLOCATE
allocated arrays (the spectrum is not processed if LastCall=.TRUE.)
Spectrum_Out(NumChans_Out) REAL Array (OUT) The output spectrum
ErrorCode INTEGER (OUT) Subroutine error code
(set to zero if the subroutine completed successfully)
ErrorMatrix (NumChans_Out, NumChans_Out) REAL Array (OPTIONAL,
OUT) Estimated error covariance matrix (see below)
4. Test Scripts
4.1. SetUp_Test_Quick.sh
&CreateEOFs
RadiancesFile = 'data_quick/RADIANCES_100Subset.dat'
CovarianceFile = 'data_quick/Cov_Test.out'
ChannelFile = 'Chans2Use_Test.dat'
MaxSpec=100
AddNoise=F
CreateCovariance=T
WriteCovariance=T
CalculateEOFs=F /
Therefore this program reads in 100 spectra from the
data_quick/RADIANCES_100Subset.dat file (which
contains 10000 simulated IASI spectra in binary format). A covariance
martrix is calculated and written to file (the binary file data_quick/Cov_Test.out). EOFs are not calculated.
&CreateEOFs
RadiancesFile = 'data_quick/RADIANCES_100Subsetx.dat'
CovarianceFile = 'data_quick/Cov_Test.out'
EigenvectorsFile = 'data_quick/Eigenvectors_Test.out'
ChannelFile = 'Chans2Use_Test.dat'
NumEOFs=100
MaxSpec=100
AddNoise=F
AddToExistingCovariance=T
CreateCovariance=T
WriteCovariance=T
CalculateEOFs=T /
Now 100 spectra are read in from a second input binary file,
data_quick/RADIANCES_100Subsetx.dat and added to
the covariance matrix calculated above. The matrix is once again
written to disk but this time the leading 100 EOFs are also calculated
for the first 1000 channels (defined in the
Chans2Use_Test.dat file).and are written to the
ASCII file
data/Eigenvectors_Test.out. The contents of
the eigenvector file are described in Section
2.2.3. This file may be compared to
Test_Runs/Eigenvectors_Test_Quick.out.gz.
&RRFilter
EigenvectorsFile = 'data_quick/Eigenvectors_Test.out' /
This program reads in radiances from two binary files:
data/RADIANCES_100_Noisy.dat and
data/RADIANCES_100.dat. The former contains
calculated IASI radiances to which random noise has been added. The
latter contains the same radiances without the noise and is used as
"truth" when calculating noise statistics.
This file may be compared to
Test_Runs/RR_Filter_Test_Quick.out. Note that
results will not be bit identical to the output in
Test_Runs/ as floating point calculations
depend in detail on the machine, compiler and compiler options used.
Agreement in the reconstructed radiances should be at least 5
sig.figs. and there should be similar accuracy in the leading
eigenvectors.
4.2. SetUp_Test.sh
5. Troubleshooting
A memory fault can arise if the called and calling subroutine
do not have matching argument types. To prevent this occuring
interface blocks have been used throughout. This is particularly
important for RR_Filter where the called
subroutine has an optional argument.
If problems are encoutered reading binary files, note
that the files supplied with this package are big-endian, so a
suitable compiler flag should be used if the machine being used is
little-endian.
Results will not be bit identical to the output in
Test_Runs/ as floating point calculations
depend in detail on the machine, compiler and compiler options used.
Agreement in the reconstructed radiances should be at least 5
sig.figs. and there should be similar accuracy in the leading
eigenvectors.
References